Proof That [d/dx](x^n) = nx^(n-1) When Exponent Is A Positive Integer

Let [f(x) = xⁿ]. By definition, the derivative would be:

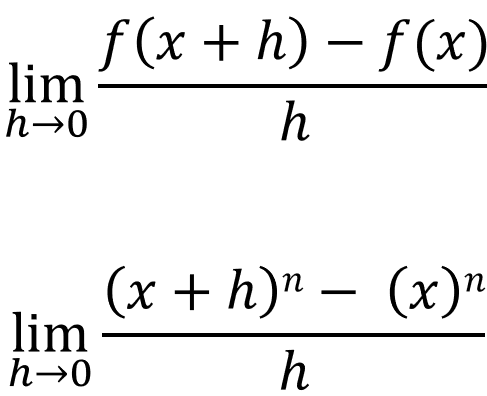
If we expand (x+h)ⁿ using the binomial theorem, we get:

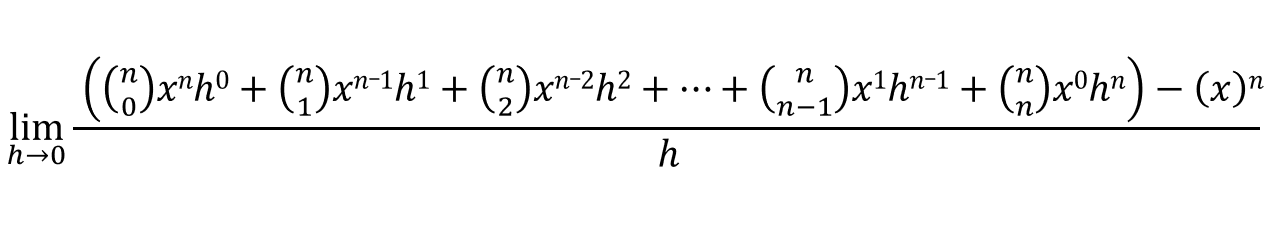
In the numerator, the first and the last terms would cancel out:

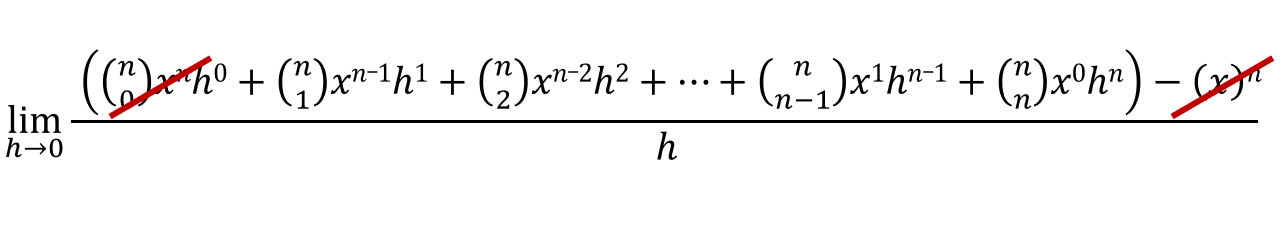
Now if you look at the numerator, the variable h exists in every term one or more times, this means we can factor out one h from every term in the numerator:

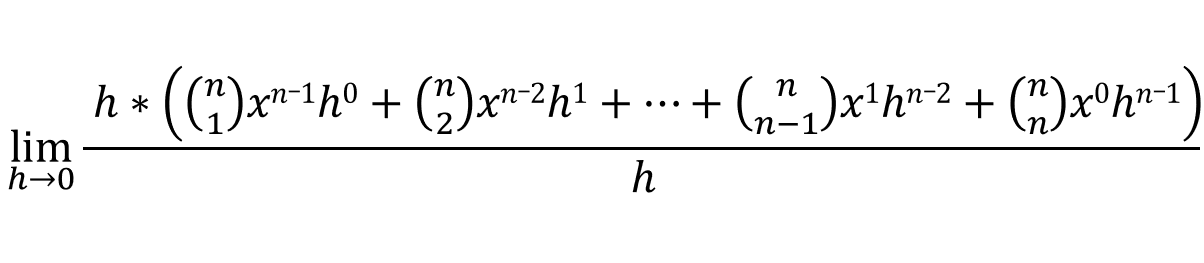
If we simplify, we get:

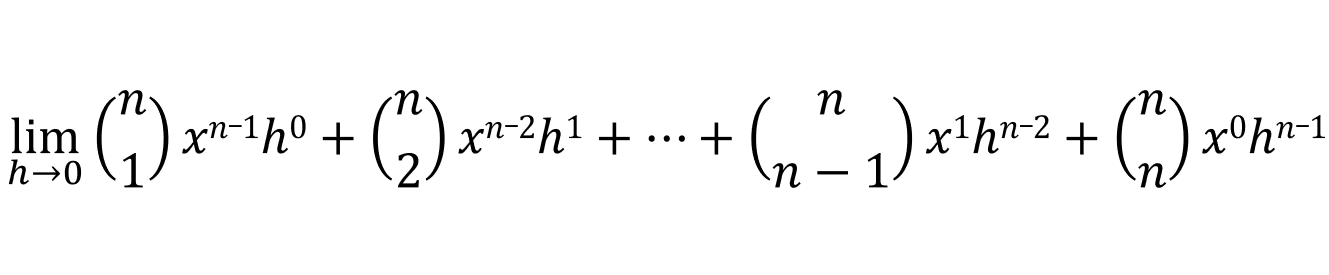
Any number to the power of zero is one as long as that number is not zero, since h goes close to zero but doesn't equal it, then [h⁰ = 1]:

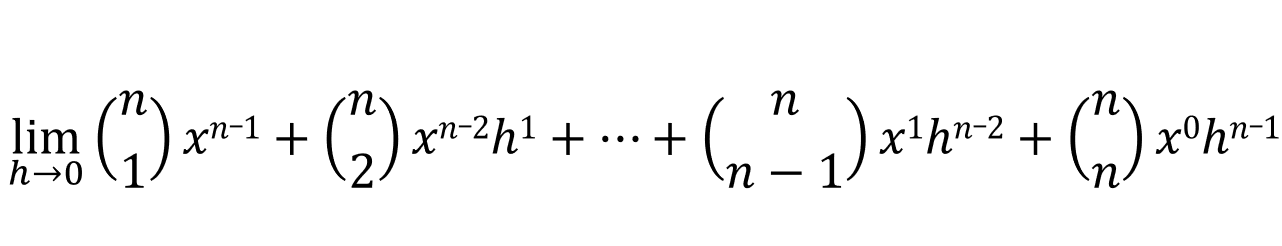
There is one rule of limits is which states that [lim_n->0 n = 0]. If every term (except for the first one) has the h variable and if h goes closer to zero, then that means all the terms except for the first one will approach zero:

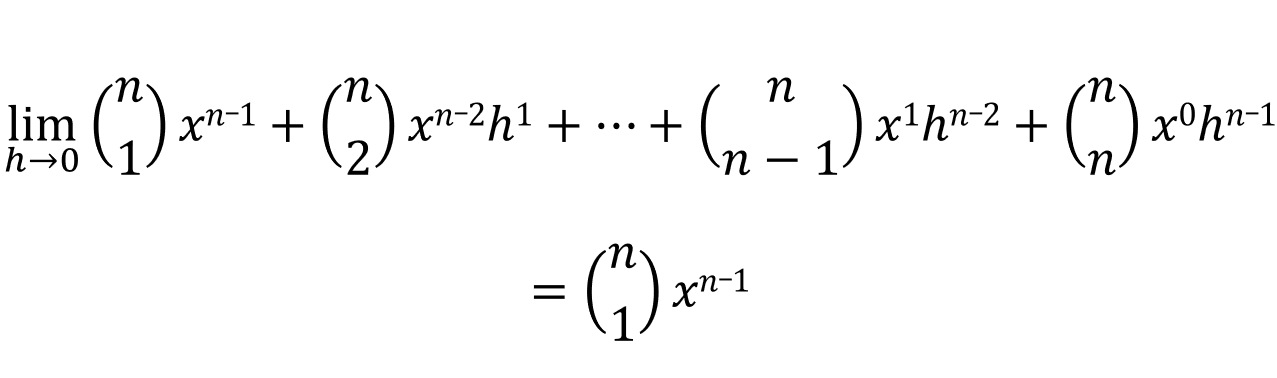
Since _nC₁ will always be equal to n (as long as n is an integer greater than one) this means that:

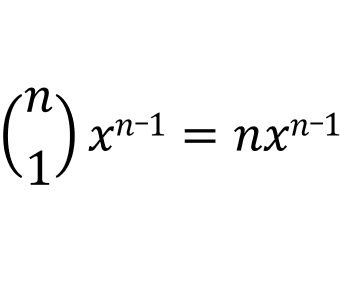
Hence, we have proven that [d/dx](x^n) = nx^(n-1) when n is an integer greater than one.